Book Report: Legacy of Dissent

Legacy of Dissent ed. by Nicolaus Mills Dissent Magazine is my favorite contemporary political journal (admittedly, of like three that I ever read). It's avowedly left-wing, so it doesn't try to be all things to all people (like some). Yet unlike many left-wing magazines, it doesn't waste your time with choir-preaching conservative-bashing that serves merely to make you feel righteous, rather than advance a discussion (like a few magazines I can think of). Rather, it devotes its energy to liberal self-critique, challenging of orthodoxies, and honest insight into what in the liberal agenda is both moral and practicable. I was vaguely aware of Dissent's history as a noteworthy anti-Communist (but pro-democratic-socialism) voice in the post-WWII landscape, so I was excited to stumble onto this collection of essays spanning the history of the magazine. Well, my overwhelming impression is: Socialist thinking was by and large a bunch of dreck, man. For an anti-Communist magazine, they spent a lot of time quoting Marx, debating what Marx really would have wanted, and cooking up their vision of what a just society would look like. Peering from the far side of the millenium, this stuff reads like so much hooey. The cultural writing, on the other hand, retains immense social and historical interest, and there are some real gems here. Paul Goodman's "Growing Up Absurd", from 1960, charts the emergence of the Beats and a whole generation of "Independents", who are not outside of the economic system, yet do not properly belong to it:

...This is the vast herd of the old-fashioned, the eccentric, and criminal, the gifted, and serious, the men and women, the rentiers, the free-lances, the infants, and so forth. This motley collection has, of course, no style or culture, unlike the organization that has our familiar "functional" style and popular culture. Its fragmented members hover about the organizations in multifarious ways — running specialty-shops, trying to teach or give other professional services, robbing banks, landscape gardening, and so forth — but they find it hard to get along, for they do not know the approved techniques of promoting, getting foundation grants, protecting themselves by official unions, lefally embezzling, and not blurting out the truth or weeping or laugh out of turn.

Cute! Another wonderful piece is Richard Wright's 1957 "White Man — Listen!", derived from his book of the same name. He wrestles with the twin facts of his existence: Black, and thus "never allowed to blend with the culture and civilization of the West"; and yet, irreconcilably, Western in his beliefs and outlook:

I have not consciously elected to be a Westerner; I have been made into a Westerner... The content of my Westernness resides fundamentally, I feel, in my secular outlook upon life. I believe in a separation of Church and State. I believe that the state possesses a value in and for itself. I feel that man - just sheer brute man just as he is - has a meaning and value over and above all sanctions or mandates from mysetical pwoers, either on high or from below... When I look out upon those vast stretches of this earth inhabited by brown, black, and yellow men — sections of the earth in which religion dominates, to the exclusion of almost everything else, the emotional and mental landscape — my reactions and attitudes are those of the West.

Though Western, Wright is not of the West:

Yet, when I turn to face the environment that cradled and nurtured me, I experience a sense of dismaying shock, for that Western environment is soaked in and stained with the most blatant racism that the contemporary world knows... Rooted in my own disinheritdness, I know instinctively that this clinging to, and defense of, racism by Western whites are born of their psychological nakedness, of their having, through historical accident, partially thrown off the mystic cauls of Asia and Africa that once too blinded and dazed them...

And I'll just end with a long excerpt from Erazim V. Kohák's "Requiem for Utopia", written after the 1968 Soviet invasion of Czechoslovakia. Kohák went into exile from Czechoslovakia in 1948, and continues to write and teach at Boston University and Charles University in Prague.

[Dubcek and his colleagues] were determined to be humane authoritarians, respecting the rights of their subjects. In their seven months in power they discovered that the idea of a humane authoritarianism, the standard illusion of welll-intentioned rhetorical revolutionists, is an illusion, a contradictio in adiecto. A humane authoritarianism would respect the freedom of its subjects, and so inevitably create the possibility of dissent and opposition. Faced with opposition, the human authoritarian faces the choice of ceasing to be authoritarian — or ceasing to be humane. Repression, whatever its overt aim, can be humane only in rhetoric — in practice it necessarily means breaking men. Czechs and Slovaks, including Dubcek, were too familiar with the logic of terror to opt for the latter alternative. After seven months, the program which started out as a program of humane communism became a program of social democracy. ... The ideals of human freedom and social justice remain valid. Democracy — democracy for blacks as well as whites, in economics as well as politics, at home as well as in remote reaches of Latin America or Eastern Europe — remains valid. Socialism, the ideal of social justice and social responsibility in industrial society, remains valid. Human and vicil rights, the right of every man to personal identity and oscial participation, all remain valid. But the utopian myths of self-proclaimed rhetorical radicals do not advance these ideals. The detour on which too many socialists embarked in 1917 is over, finished, discredited, revealed as an exhiliarating, aristocratic, and ultimately reactionary social sport, not the radical social progress it claimed to be. The task that remains is the work of social progress — not the aristocratic sport of revolution, but the solid work of redical, deep-rooted transformation of society. Men may still demand their daily dose of illusion, the exhilaration of revolution or "confrontation" rather than the down-to-earth facts and figures of a Freedom Budget; but those who cater to this demand can no longer do so in the name of social progress — or in the name of socialism. Utopia is dead. Czechoslovakia has been a graveyard of illusions.

Evolution Songs

Some theories of origins have inspired generations of musicians. Darwin's theory of evolution has not. This may be because humans have a hard time emoting about an impersonal process that unfolds over millions of years. Or it could be because there is no enormous institution extracting tithes from the entire population and commissioning artistic works that perpetuate its worldview. In any case, I do know of two pretty neat songs that are about evolution, and thought I'd share them with you. You can listen to lo-fi previews of the songs, which hopefully won't get me in trouble.

	Gentle Arms of Eden Dave Carter & Tracy Grammer Drum Hat Buddha	[ listen to preview ] [ Buy from iTunes ] [ read the lyrics ]
	I Come From Water The Toadies Rubberneck	[ listen to preview ] [ Buy from iTunes ] [ read the lyrics ]

Puppy Love

They have such an understated, charming way of expressing their affection for one another. Click for a too-long movie I learned yesterday evening that they don't get bored after 90 minutes of this. I tried suggesting playing with Legos or something more constructive, but they went right back to tug. What would be a better use of the audio track — remixed into a techno song, or sold as a home security device?

Zombie Watch

David Chalmers has started a blog (via Matthew Yglesias al Alina Stefanescu al Forking Paths). If you're unfamiliar with him, Chalmers is one of two or three people responsible for wresting control of the discussion about consciousness from the epiphenomenalists. I've seen him talk a few times and he's quite engaging, so the blog will be worth following. Apparently these days he's working on something called "two-dimensional modal logic", which according to this book description that Chalmers links to, is part of a movement that

[wishes to] revive descriptivism in the philosophy of language, internalism in the philosophy of mind, and conceptualism in the foundations of modality. ... In the last twenty-five years, this attack on the anti-descriptivist revolution has coalesced around a technical development called two-dimensional modal logic that seeks to reinterpret the Kripkean categories of the necessary aposteriori and the contingent apriori in ways that drain them of their far-reaching philosophical significance.

Well. Glad that's clear. Perhaps when chapter two is finished our philosopher friend can explain?

English Practice

Okay, I probably should have known many of these words. But that's why it's practice... ordure: excrement; or, something morally offensive. [Latin horridus]

"That kind of rig, a man'd die settin' in his own, uh, ordure long before they got around to stretching his neck." - p13, The Confessions of Nat Turner

chattel: An article of moveable personal property (as distinguished from real estate). [Latin capitalis]

"The point is that you are animate chattel and animate chattel is capable of craft and connivery and wily stealth... Because that's how come the law provides that animate chattel like you can be tried for a felony, and that's how come you're goin' to be tried next Sattidy." - pp21-22, The Confessions of Nat Turner

sedulous: persevering, assiduous.

Right now I had this other bitterness to contend with, the knowledge of which for ten weeks I had so sedulously shunned... - p23, The Confessions of Nat Turner

fagot: A bundle of sticks tied together. [Greek phakelos, bundle]

They moved with quick and sprightly motions... piling twigs and sticks and fagots high in their arms against their bodies. - p40, The Confessions of Nat Turner

bruit: a rumor or report; in medicine, an abnormal sounds heard in auscultation [Old French bruir, roar]

"For several years now there has come to my attention wondrous bruit of a remarkable slave, ..., who had so surpassed the paltry condition into which he had been cast by destiny that — mirabile dictu — he could swiftly read from a difficult and abstract work in natural philosophy... - p66, The Confessions of Nat Turner

folderol: Foolishness, nonsense

"I do think Boysie's sermon was most inspiring, don't you, little Miss Peg?" "Oh Mother, it's the same old folderol, every year! Just folderol for the darkies! - p104, The Confessions of Nat Turner

gallus: suspenders.

He blinks steadily, and with his other hand he adjusts one gallus on his shoulder... - p149, The Confessions of Nat Turner

Have a merry snowstorm, everybody.

Transductive Inference

The brilliant, if eccentric and self-congratulatory Vladimir Vapnik has been trumpeting a major shift in the scientific method, and perhaps our epistemological stance, over the past few years. Whether or not Vapnik gets his revolution, at the very I least I'll wager you will see "transductive inference" gain increasing attention as his ideas trickle out from statistical learning theory to other intellectual fields. So what's it all about? The goal of science (it can be argued) is the accurate prediction of future or novel events. Since the days of Aristotle, and especially since Bacon, the essential means of scientific inference is induction. Bearing Hume's warnings in mind, we generally follow this familiar process:

• Make a number of observations
• Induce a general law (or mathematical function) that we think is generating the phenomenon.
• Use the law to make predictions about future phenomena.

To simplify the discussion, let's restrict ourselves to a problem of classification. You are encountering a steady stream of objects -- say, liver cells. First you get a batch (the "training set") which are labelled in two groups, say "normal" vs "cancerous". Your goal (especially in applied science) is simply to devise a rule by which you can accurately classify future cells (the "test set") as normal or cancerous. To make your classification, you measure various characteristics of the liver cells; for example, size, color, mitotic activity, expression level of various proteins, etc. For simplicity, let's suppose you measure just two characteristics, size and the level of "protein A". 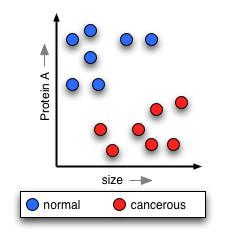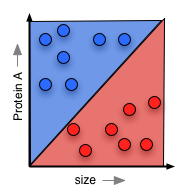You could draw a graph plotting all of the cells on these two characteristics, coloring the normal cells blue, and the cancerous red: Now, if you're doing normal scientific induction, you'll look at this training data and try to posit a simple rule that will explain the data, and help you understand nature's "hidden rule" that makes some cells cancerous and others not. In classical statistics, this means you come up with a function that will "paint" part of the surface red, and part blue. This paint forms your prediction about any cell that lands in each region: Vapnik helped found the field of computational learning theory, in which one takes a slightly different approach. Rather than trying to guess nature's "hidden rule", you worry solely about minimizing the error your function will have when you test it against more liver cells. The surface-painting you come up with might not be parsimonious or a sensible guess about what nature is doing, but if it is a successful predictor, that's fine. Now comes the upheaval that is transductive reasoning. Vapnik has established mathematically that you pay a certain price in the accuracy of your predictions by generalizing to pain the entire surface either red or blue. So his idea is this: rather than first doing induction to posit a general rule, then making predictions about new liver cells as you see them, you simply transduce to make a prediction about each new cell as you see it, based on everything you've seen before. You don't get a simple rule that you can explain or write down -- all you get is a prediction each time. Vapnik has demonstrated that transduction will always perform better than induction on a given problem. So this leaves us with this abbreviated scientific method, in which we:

• Make a number of observations
• Use transduction to make predictions about new phenomena as we encounter them.

At least in particular problems in applied science, this really could be an upheaval. Who cares about having tidy theories and approximations of nature's mysterious inner ways if we can always have the better predictor? As a general approach to natural science, however, it's problematic. We induce models that measure the importance of Protein A not just so that we can make great predictions of whether a cell is cancerous. We also want to know whether we should investigate Protein A more deeply, learn about its structure and function, or invent drugs to mimic or inhibit it. Transduction doesn't help us make these decisions, and so we will always need some inductive reasoning along with our transductive predicting.

---

Thus far, the potential impact of transduction has only begun to make an impression on the philosophical community. I haven't found any discussion of it in the philosophy of science, but that could be because I don't understand the current problems and arguments in that field. Gilbert Harman, a former professor of mine, is making an intriguing application of transduction to moral reasoning in a paper to be published later in 2005 (RTF, HTML). Essentially, Harman asks whether, if transduction can offer superior classification, we shouldn't attempt to use transduction to "classify" moral actions into "should do" and "shouldn't do." We would sacrifice the formation of inducing general moral principles which we could elaborate and trasmit, but we would (presumably) gain "better" moral decisions. Is it worth giving up comprehensible theories for better predictions? Will we see transductive inference gain a foothold in economics, finance, the social sciences? It's one to watch.

Graph Theory Tidbits

You are at a cocktail party. People are introducing themselves and shaking hands. Since parties make you uncomfortable, you lean against the wall. Rather than having meaningful human interaction, you can do a little graph theory instead, which is much more fun. With a little thinking, you can derive two interesting conclusions:

1. At least two people shook the same number of hands.
2. An even number of people shook an odd number of hands.

The first result rests on the wonderfully named "pigeonhole principle." Consider what it would take for no two people to shake the same number of hands: each person would have his or her own unique "shake-count". We consider each shake-count a "pigeonhole", because it's like a slot that we fill with a person. So Aziz shook zero hands, Bob shook one hand, Carmen two hands, etc. With n people, we could assign "shake-counts" from 0 all the way up to Zaphod who shook n-1 hands (assuming we don't permit someone to shake hands with himself). This is n different shake-counts, so it seems we could indeed have n people, each with their own shake-count. But consider what it implies for Aziz to have a shake-count of zero: outcast that he is, he didn't shake anyone's hand at all. Zaphod, with a shake-count of n-1, shook the hand of everyone at the party. But Aziz and Zaphod can't be at the same party: if Zaphod succeeds in shaking everyone's hand, then Aziz can't have shook no hands, and vice-versa. Hence any single party has only n-1 pigeonholes for shake-counts. When you try to stick n people in n-1 pigeonholes, you'll end up with at least two people in the same pigeonhole. So at least two people shook the same number of hands. Hoorah!

---

The second result is even more kooky sounding, but it also follows from very simple principles. Consider the total of each partygoer's personal "shake-count". Each handshake involves two people, so the sum of everyone's shake-counts must equal twice the total number of handshakes. (Think about that one for a sec to make sure you get it). This means that the sum of shake-counts is an even number. Now, consider the people who shook an even number of hands: the sum of their shake-counts must be an even number too, since when you add together even numbers you get even numbers. This means that the remaining sum of shake-counts, the sum of the shake-counts of people who shook an odd number of hands, must also be an even number. Now, to get an even number by adding up odd shake-counts, there must be an even number of such people. (Simple example: 3 + 3 = 6 (two people, even sum), but 3 + 3 + 3 = 9 (three people, odd sum). So, there is always an even number of people that have shaken an odd number of hands! Happy Graph Theory Awareness Week!

Maltheism

Since the tsunami has everyone in a theodicic frame of mind, and perhaps because I'm reading this book, I have maltheism on the mind today. It's a possibility one oughtn't discount out of hand: God exists, and is evil. For a brief introduction to the idea, wander over to the Maltheism blog, which I stumbled onto today. Start at the bottom and scroll up. There's a sad sweet story embedded there, and I offer my condolences to Craig. To frame the issue from the top, we begin with whether there is a divine presence. Supposing one decides that there is (whether from miracle, first cause, design, etc.), one next faces the questions of whether God is one or many, and the ethical alignment of those god(s). In a class on the problem of evil that I took from Mark Larrimore, I remember we discussed dualist beliefs such as Manichaeism and Zoroastrianism, i.e. that there are opposed good and evil supernatural influences in the world. Polytheist religions often have gods of a mixed character; one need only inspire the wrath of Juno once to understand that the divinities are fickle. And of course, some versions of Christianity place more emphasis on the existence of Satan, a divine but not omnipotent figure who works for evil. All of these systems capture a feeling of dynamic struggle that resonates with me, and apparently with many others throughout history. Against the "struggle" view are the twin possibilities of a single beneficent God, and a single malevolent God. The former seems to me to compel a Panglossian hypothesis that we live in the best of all possible worlds. To maintain that this the best of all possible worlds, one must undertake a series of contortions to explain how just this much suffering is required, lest we live in a still worse world. Such lines of argument strain my imagination to its limit, and don't particularly resolve the emotional problem of evil. Instead, they feel like a theological neat trick that seems more designed to defend God than to help the human. Or, we consider the (historically rare) maltheist position: there is a malevolent God. An omnipotent, malevolent God immediately poses a complementary "problem of good": how does any good exist in the world? As we discussed in Larrimore's class, most definitions of evil take the form of evil as a privation of good, i.e. a deficit of a good. So the existence of at least some good seems to be required. Now, is this really the worst of all possible worlds? Do we have a malevolent, omnipotent God coaxing things along to be just good enough to keep the wheels of life turning around, so as to permit the next generation's catastrophe? I admit this strains credulity. Surely there could be worse possible worlds, ones of unmitigated suffering (perhaps punctuated by 30 minute stretch breaks to remind us how bad we have it). But framing this problem against its converse suggests the outline of an antinomy to weigh with the others. This leaves me with the possibility of a malevolent God that is not omnipotent. Rather, there simply exists some dark being out there, throwing us curveballs and tidal waves. What I like about this proposition is that it that restores the focus on human action. Rather than wondering whether we're pleasing God, and how best to avoid his wrath, we simply assume he's out to get us, and so must strive in every way possible to ward Him off. We may just be ant underfoot, but we've got a bit of maneuvering room, and so must get busy to keep our fragile way of life together.

English Practice

You know a word is a tough one when the first Google result containing the word is the dictionary entry. I wonder if one could assemble a complete list of such words, used primarily in sentences defining or discussing the meaning of the word itself... Some English practice for us all: irenic: Promoting peace; conciliatory.

Among the more irenic critics [of Burnet's flood geology] was Robert Hooke... - The Biblical Flood p69

palistrophe: synonym for chiasmus; A rhetorical inversion of the second of two parallel structures.

British evangelical scholar Gordon Wenham has made a case for the coherence and unity of the flood narrative on the basis of a perceived extended palistrophic or chiastic structure in which the first item matches the final item, the second item corresponds to the penultimate item, and so on, so that the second half of the story is a mirror image of the first half. - The Biblical Flood p238

raiment: Clothing; garments.

The national raiment, in [Vladimir Jabotinsky]'s formulation, had to be unsullied by foreign admixtures and universalistic notions such as socialism. - The Legacy of Dissent p138

tribune: A protector or champion of the people (from Latin tribuna, raised speaking platform)

...since even [Tom Wolfe's character from Bonfire of the Vanities] Kramer's father "had no interest in left-wing politics," a reader might suppose that father's socialism, too, was merely half-remembered and that, in the Kramer family, grandfather, the oppressed immigrant garment worker, was socialism's truest tribune. - The Legacy of Dissent p212

Aesthetic != Fun

Just a quick reminder that great literature often makes lousy life. But Leonardo was so enchanting! Of course, it's the third-leading cause of death for teenagers (and increases with age). Perhaps one day we'll really be up to talking about it.